Huffman
2 – Principe
L'idée principale de Huffman est de modifier la séquence binaire des caractères en fonction de leur fréquence.
Les 256 caractères sont codés sur 8 bits. Huffman propose de modifier ce codage de la manière suivante : Plus la fréquence du caractère est grande, plus la séquence binaire est petite. Ainsi, on "gagne" de la place sur la totalité du fichier.
3 – Compression
La première étape consiste à compter le nombre de caractères et leur fréquence.
On utilise une liste chaînée dans laquelle on range, chaque caractère présent dans le fichier, par ordre décroissant de fréquence et de code ASCII.
A partir de cette liste, on crée un arbre binaire dont on tire la table de Huffman qui fait correspondre chaque caractère différent à son nouveau code binaire.
Il ne reste plus qu'à réécrire les caractères du fichier en les remplaçant par leur nouvelle séquence binaire et en les regroupant par paquet de 8 bits.
3.1 – Liste chaînée
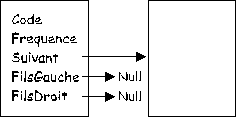
La liste chaînée est constituée de cellules dont la structure est la suivante :
type Cellule is record
Code : integer;
Frequence : natural;
Suivant : Pointeur;
FilsGauche : Pointeur;
FilsDroit : Pointeur;
end record;
Code représente le code ASCII du caractère.
Frequence, le nombre de fois qu'il apparaît dans le fichier et Suivant pointe sur la cellule suivante.
FilsGauche et FilsDroit pointent sur les cellules gauche et droite dans l'arbre (Ils serviront à la création de l'arbre, ils sont initialisés à Null).

Pour détecter la fin du codage, nous ajoutons un caractère de fin de fichier unique dont le code ASCII est 256.
Pour créer la liste, on lit tout le fichier caractère par caractère que nous stockons en mémoire dans un tableau de fréquences, dont les indices représentent les codes ASCII.
Puis on construit la liste en créant et en ajoutant une à une les cellules en tête de liste.
3.2 – Tri
Pour préparer l'étape suivante, il faut trier la liste en ordre décroissant de fréquence et de codes ASCII.
Le principe est de trier, dans un premier temps, la liste en ordre décroissant de fréquence par la méthode de sélection puis de scinder cette liste en deux.
La première contenant les premières cellules de fréquences égales, la seconde le reste.
On trie ensuite par sélection la première liste en ordre décroissant de code ASCII.
On répète autant de fois l'opération qu'il y a de fréquences différentes sans oublier de concaténer les "bouts" de liste triées.
Cette structure de tri se traduit dans le code par 5 procédures dont 4 sont déclarées dans la procédure principale TriListe.
Procedure TriListe(Liste : in out Pointeur) is
~ ~ ~
procedure TriListeFrequence(Liste : in out Pointeur) is
~ ~ ~
procedure TriListeCode(Liste : in out Pointeur) is
~ ~ ~
Procedure Scission(Liste : in out Pointeur; Liste1 : out Pointeur; Liste2 : out Pointeur) is
~ ~ ~
Procedure Concatenation(Liste : in out Pointeur; Liste1 : in Pointeur) is
~ ~ ~
Pourquoi avoir choisi le tri par sélection et non pas un tri rapide comme le tri fusion, le tri par Tas ou encore le tri rapide ?
On a vu que, pour 250 éléments à trier, il y a un facteur 8 en temps de traitement entre un tri rapide et le tri par sélection.
En ce qui concerne la compression, nous sommes amenés à trier une fois (la liste) 257 éléments, plus (l'arbre) une fois 256 éléments, plus une fois 255 éléments, plus … ,plus une fois 3 éléments, plus une fois 2 éléments.
Dans le pire des cas, les 257 caractères ont la même fréquence. On multiplie donc par 2.
Ce qui fait approximativement 3 minutes contre 30 secondes pour un tri rapide. (Voir le cours de structure de données de Mme Costa).
Nous verrons dans le chapitre 5 qu'en réalité les temps de traitement sont bien meilleurs que cela.
Aussi, mon choix n'a pas été déterminé par le gain de temps potentiel mais plutôt par la simplicité de mise œuvre du tri.
3.3 – Arbre
Pour redéfinir les séquences binaires des caractères, on utilise la structure d'un arbre binaire. Sa construction à partir de la liste chaînée triée est très simple.
On sait que les deux dernières cellules ont les fréquences les plus petites. Il suffit de créer une cellule selon la règle suivante :
Le père pointe sur les deux fils qui ont les plus petites fréquences. En cas d'égalité on choisit le caractère de code ASCII inférieur. Le père contient le code ASCII le plus petit des deux et la somme des fréquences des deux fils. Ainsi, de proche en proche, on construit l'arbre.
FilsDroit pointe sur la cellule de fréquence plus petite ou, en cas d'égalité, sur la cellule de code ASCII le plus petit.
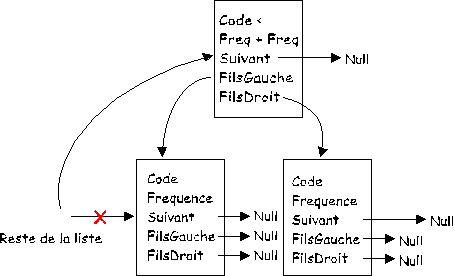
L'instruction qui réalise cela est :
CPP.Suivant := new cellule'(CP.Code,CC.Frequence + CP.Frequence,Null,CP,CC);
Voir la procédure CreationArbre pour plus de détails.
La nouvelle cellule devient la cellule de fin de liste. Il suffit de trier cette nouvelle liste et de recommencer jusqu'au pointeur de début de liste qui devient la racine de l'arbre.
3.4 - Table de Huffman
L'arbre étant construit, l'étape suivante est d'établir la table des correspondances par un algorithme de parcours en profondeur.
Par convention, on associe la valeur 0 aux arcs de gauche et 1 à ceux de droite.

L'idée est d'utiliser une procédure récursive qui teste le noeud en cours. Si c'est une feuille, on range le code et sa longueur dans un tableau de cellules constituées d'un tableau de bits et d'un champ longueur.
Ainsi chaque caractère se voit attribué une nouvelle séquence binaire.
Dans le pire des cas, l'arbre a 257 feuilles et tous les nœuds sont sur une même branche.
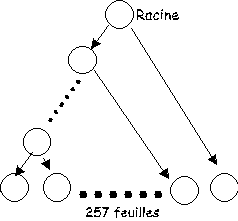
Ce cas justifie la déclaration du tableau de bits suivante :
type Bit is array (1..257) of natural range 0..1;
type Objet is record
Longueur : natural := 0;
Binaire : Bit := (others => 0);
end record;
type InfoCaractere is array (0..256) of Objet;
3.5 – Codage
Le codage consiste à lire le fichier original, caractère par caractère, à appliquer la table de Huffman et à écrire les nouveaux caractères de façon fluide.
Pour ce faire, on utilise un tampon qui constitue les séquences binaires en paquets de huit bits.
Une fois que le tampon est plein, on transforme son contenu en caractère par une fonction qui code du binaire en décimal (la fonction BinaireDecimal).
Puis on écrit le caractère dans le fichier compressé.
La procédure codage écrit d'abord un "repère" en début de fichier qui permet de savoir si c'est un fichier compressé.
J'ai choisi "Huf" en supposant qu'il était très peu probable de rencontrer ce mot en début de fichier. Ensuite, elle écrit le nom du fichier original puis sa structure. C'est à dire la fréquence de chaque caractère.
Cette dernière action permettra de reconstruire la liste, puis l'arbre lors de la décompression.
Evidemment, cela prendra un certain temps, le mieux eut été de sauvegarder l'arbre. Je ne l'ai pas fait pour 2 raisons :
La première est que l'utilisation d'un tableau diminuerait le taux de compression. En effet, la structure de l'arbre prendrait plus de place que les fréquences.
La deuxième est que les processus qui permettent d'aboutir à la table de Huffman ont une durée négligeable par rapport aux entrées/sorties sur les fichiers.
4 – Décompression
La décompression utilise pratiquement les mêmes procédures que la compression. Nous avons vu que la fréquence de chaque caractère est sauvegardée dans le fichier compressé. Lors de la décompression, ces fréquences vont servir à créer la liste chaînée identique à celle de la compression.
Aussi, les fonctions de tri et de création d'arbre vues plus haut servent de nouveau.
3 procédures ont été ajoutées :
FormatFichier.
NomOriginal.
Decodage.
Comme son nom l'indique FormatFichier vérifie que le fichier à décompresser est compressé. NomOriginal récupère le nom du fichier initial.
Le décodage est l'opération inverse du codage. Les caractères lus doivent être convertis en séquence binaire puis segmentés en fonction de l'arbre et enfin écrits dans un fichier.
4.1 – Décodage
On a vu plus haut que la décompression recréait l'arbre initial à partir des fréquences des caractères.
Le décodage consiste à lire les caractères du fichier source un à un, de les passer dans la fonction DecimalBinaire qui convertit un caractère en séquence binaire, puis, de parcourir l'arbre en partant de la racine de la façon suivante : si c'est un 0 on prend l'arc de gauche, si c'est un 1 celui de droite jusqu'à "tomber" sur une feuille qui nous donnera le "vrai" caractère.
Le caractère 256 indique la fin du traitement.
La procedure Decodage réalise cela.
5 – Erreurs
Les erreurs sont liées aux opérations sur les fichiers.
NAME_ERROR : indique que le nom de fichier est erroné ou que le fichier est manquant.
DEVICE_ERROR : indique que le device demandé n'existe pas ou que le fichier n'est pas sur ce device.
CONSTRAINT_ERROR : concerne le nombre d'arguments passés. Si ce nombre est trop petit ou trop grand, l'exception est levée.
USE_ERROR : indique que l'on essaie d'écrire sur un support ou un fichier protégé en écriture.
MAUVAIS_FORMAT : est levée lorsque l'on essaie de décompresser un fichier non compressé.
6 – Interface
L'exécutable admet 1 argument au minimum et 3 au maximum.
Le premier argument est une commande : le "c" pour compressé, le "d" pour décompresser ou le "?" qui affiche l'aide à l'écran.
Dans le cas d'une compression, le deuxième argument est le nom de fichier à compresser. Il doit être obligatoirement suivi du troisième argument qui indique le nom du fichier compressé.
En revanche, s'il s'agit d'une décompression, le deuxième argument est le nom du fichier compressé. Le troisième est le répertoire de destination.
7 – Tests
Les tests ont été effectués sur une machine monoprocesseur (AMD 300 Mhz) possédant 64 Mo de RAM sous Windows 95. Aucune autre tâche ne s'exécutait sur la machine.
t le taux de compression :
t = 100 – (Nombre de caractères destination/Nombre de caractères source) * 100.
Tp le temps d'exécution partiel :
Création de la liste + les tris + création de l'arbre + création de la table de Huffman.
T le temps d'exécution total :
Tp + le temps des entrées/sorties sur les fichiers.
I – Tartuf.txt
Fichier non compressé : 103 506 Octets.
Avec Projet (Ada):
Fichier compressé : 62 729 Octets.
t = 39%.
Tp = 1 seconde.
T = 5 secondes.
Avec projet (C):
Tp = 0.3 secondes.
T = 1 seconde.
Avec Winzip :
t = 62%.
T ~ 2 secondes.
II – Wdmain8.hlp
Fichier non compressé : 2 050 344 Octets.
Avec Projet (Ada):
Fichier compressé : 1 775 335 Octets.
t = 13%.
Tp = 1 seconde.
T = 106 secondes.
Avec projet (C):
Tp = 0.3 seconde.
T = 40 secondes.
Avec Winzip :
t = 31%.
T ~ 15 secondes.
Taille de l'exécutable:
Ada : 607 Ko.
C : 30,7 Ko.
Ces résultats montrent que les efforts de conception se porteront sur les entrées/sorties des fichiers plutôt que sur le tri.
On verra dans le chapitre suivant comment améliorer ces résultats.
8 – Améliorations
Les améliorations possibles portent sur le taux de compression et la rapidité d'exécution.
I – Taux de compression
D'après la relation du taux de compression, le seul moyen de diminuer t est de diminuer le nombre de caractères destination.
On sait que le format du fichier compressé comporte 3 zones :
Le repère, que nous pouvons supprimer : on gagne 3 Octets.
Le nom de fichier : on gagne ~ 20 Octets.
La structure du fichier source : sur ce point on peut gagner 256 Octets en supprimant les blancs devant chaque nombre. Ils ont été crées par la fonction de conversion d'un nombre en string. Il semblerait que cette fonction prenne en compte le signe du nombre.
Une solution serait de sauvegarder la structure du fichier source d'une autre façon.
On peut déjà estimer le nombre d'octets maximal ajoutés par notre solution :
255 (caractères) * 7 (9 999 999 occurrences) + 1 (caractère de fin de fichier) = 1786 Octets.
Dans le meilleur des cas on gagne 2065 Octets. Ce qui est peu par rapport à la taille d'un fichier susceptible d'être compressé.
II – Rapidité
On a vu que la rapidité d'une compression était surtout liée aux entrées/sorties du fichier. En effet, l'opération fait que nous lisons entièrement 2 fois le fichier, caractère par caractère, or l'accès au disque se compte en millisecondes. En revanche, l'accès à la RAM est de quelques nanosecondes, c'est à dire 1 000 000 fois moins long.
Les améliorations possibles seraient de ne lire qu'une seule fois le fichier et de le lire ligne par ligne.
A - La lecture par blocs
A ma connaissance, le langage Ada ne permet pas de lire par blocs d'octets. En revanche, C le permet. Le gain de temps n'est pas spectaculaire. Les tests effectués montrent que la valeur d'un bloc est optimale à 4096 octets (on gagne moins d’une seconde à la compression pour le fichier wdmain8.hlp) . En dessous, il n'y a pas d'amélioration significative, au-dessus, le quotient "Vitesse/Place mémoire" est plus faible.
Cette faible différence est probablement due au fait que la lecture d’un caractère par programmation se traduit par la lecture du secteur par le système.
En outre, le code est complexifié et la mise au point est délicate. J'ai modifié la fonction ChargementCaractere que vous pouvez consulter à l'annexe A.
B - La lecture du fichier
Il est possible d'améliorer la vitesse de compression en ne lisant qu'une fois le fichier source. Le taux de compression serait (cette idée n'a pas été implementée) certainement très diminué.
L'idée est de lire un bloc de n octets et d'en tirer des statistiques sur le nombre de chaque caractère, ainsi on en déduirait l'arbre, on coderait le bloc, puis le reste des caractères. Pour les fichiers inférieurs ou égaux à ce bloc, la méthode de Huffman est respectée.
Le cas où certains caractères ne seraient pas dans le bloc, mais plus loin dans le fichier, nous oblige à les mettre à 1.